Calcul du volume et de la surface d'un cône
Le cône est un volume délimité par une base circulaire et une surface conique. Pour en calculer son volume et ses surfaces il est nécessaire de connaître le rayon de la base et la hauteur prise perpendiculairement à la base.
Calcul du cône
| Périmètre de la base : |
6,28 m |
| Surface de la base : |
3,14 m2 |
Volume du cône : |
2,09 m3 |
Les résultats ci-dessous sont valables seulement dans le cas où le sommet est à la perpendiculaire du centre de la base, c'est à dire dans le cas d'un cône droit.
| Surface latérale cônique : |
7,02 m2 |
| Surface totale du cône : |
10,17 m2 |
| Rapport volume / surface totale : |
0,21 m3/m2 |
| Apothème : |
2,24 m |
| Angle de construction : |
161,00 ° |
Voir le schéma de la construction du cône ci-dessous |
Surface du cône
Pour une même hauteur et une même surface de la base, le volume reste constant, que le sommet soit à la perpendiculaire de la base ou non. Par contre la surface latérale cônique sera minimale dans le premier cas et augmentera d'autant plus que le sommet sera décalé par rapport à cette perpendiculaire. C'est pourquoi les résultats sont ventilés en deux parties. La première étant valable pour les deux cas, la deuxième seulement pour le cône droit.
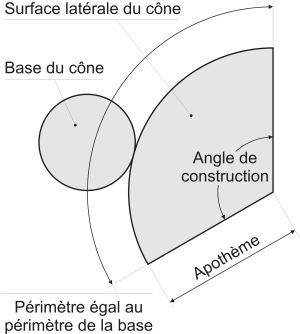
Construction d'un cône circulaire droit dit encore cône de révolution
Le cône circulaire droit a la particularité d'avoir son sommet à la perpendiculaire du centre de la base, ce qui le rend facile à fabriquer à partir d'une feuille de papier, de tôle ou autres matériaux plans et flexibles. Pour réaliser le patron d'un cône circulaire droit, tracez le cercle de base (si nécessaire pour fermer le cône). Accolez à celui-ci une portion de cercle dont le rayon est égal à l'apothème (segment qui relie le sommet au périmètre de la base du cône) et la partie circulaire du périmètre est égale à la circonférence du cercle de base - voir schéma ci-dessous.
Liste des pages de calculs
Argent
Automobile
Construction
Conversion
Divers
Electricité
Hydraulique
Informatique
Mathématiques
Arithmétique
Géométrie
Calculs des surfaces
Triangles
Quadrilatères
Surfaces circulaires
Calculs des volumes et de leurs surfaces
Calculs des développantes
Trigonométrie
Mécanique
Santé
Sciences
Usinage