Calcul du train épicycloïdal
Calculer le rapport de multiplication ou démultiplication d'un train épicycloïdal peut paraître assez... tordu  . Voici une page de calcul pour vous simplifier la vie.
. Voici une page de calcul pour vous simplifier la vie.
Un train épicycloïdal est un système d'engrenages particulier, constitué d'une couronne planétaire, d'un porte-satellites supportant plusieurs satellites et d'un pignon planétaire.
Calcul du train épicycloïdal
Retenez bien la terminologie du train épicycloïdal, elle est essentielle pour une bonne compréhension des calculs et de leurs résultats.
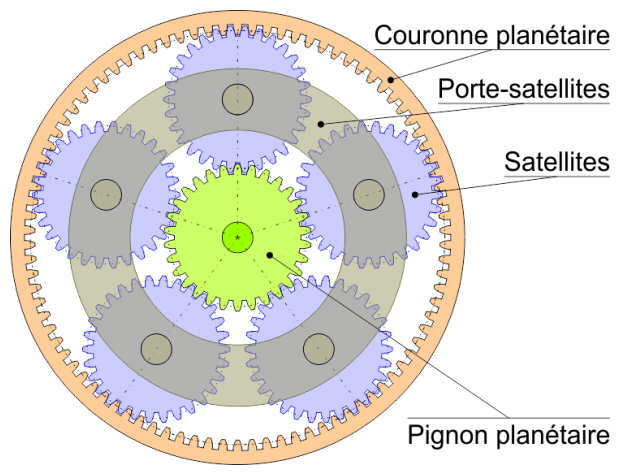
Terminologie du train épicycloïdal
Couronne planétaire
C'est une couronne dentée ayant la particularité d'avoir les dents dont le sommet est orienté vers l'intérieur.
Porte-satellites
C'est un plateau comportant les axes autours desquelles tournent les pignons satellites. Il peut être fixe ou mobile. S'il est fixe, alors le système se comporte comme un inverseur de sens de rotation, et le rapport de multiplication ou démultiplication est simplement fonction du rapport entre le nombre de dents de la couronne et le nombre de dents du pignon planétaire, tout au moins dans le cas d'un train épicycloïdal simple.
Satellites
Ce sont les pignons montés sur le porte-satellites, qui entrainent (ou se font entrainer par) ce dernier lorsqu'il est mobile. Lorsque le porte-satellites est fixe, les pignons satellites tournent seulement sur eux-mêmes.
Pignon planétaire
C'est le pignon central, placé au coeur même du système.
Diamètre primitif
Le diamètre primitif prend sa mesure à la moyenne des points de contact des dents de deux éléments engrenés.
Module
Le module n'est pas spécifique aux trains épicycloïdaux, mais aux engrenages en général. Il correspond à la dimension standardisée d'une dent d'engrènement. Un module "1" donne un entraxe de 3,14 millimètres entre 2 dents. Un module "2" donnera ainsi un entraxe de 6.28 millimètres. Cet entraxe est mesuré sur le diamètre primitif, en suivant la courbe.
En connaissant le module et le nombre de dents, on obtient directement le diamètre primitif par une simple multiplication. Par exemple : un pignon de 20 dents de module "2" aura un diamètre primitif de 40 mm.
Le module est généralement un nombre entier, ou quelquefois un sous-multiple simple (ex : 1,5). Il ne comporte pas d'unité.
Quelques modules standards : 1 - 1,5 - 2 - 2,5 - 3 - 4 - 5 - 6
Avantages du train épicycloïdal
Les engrenages par trains épicycloïdaux procurent certains avantages intéressants tels que :
- Encombrement et poids moindres à puissance et couples équivalents
- Couples de transmissibles plus élevés
- Meilleure répartition des forces sur les pignons réduisant grandement les efforts supportés par les roulements
- Un meilleur rendement, ou plutôt, des pertes moindres (à condition d'une fabrication de qualité)
- Arbres d'entrée et de sortie placés sur le même axe
Inconvénients du train épicycloïdal
Malheureusement ce type d'engrenages comporte aussi quelques inconvénients :
- Coût de fabrication plus élevé
- Hyperstatisme, nécessitant une qualité de fabrication irréprochable
Nombre maximal de pignons satellites
Selon la configuration, il est possible de placer plus ou moins de pignons satellites sur le porte-satellites. Plus ils sont nombreux, plus le couple transmissible pourra être important. Cependant, il y a une limite maximale qu'il n'est pas possible de dépasser. Vous la retrouverez dans les résultats.
Calculer la vitesse de sortie d'un train épicycloïdal
La vitesse de rotation de sortie d'un tel système d'engrenages est fonction de l'élément entraînant, de la partie fixe et de l'élément de sortie. Entrez la vitesse de rotation initiale et choisissez l'élément sur lequel elle s'applique. Les résultats afficheront les vitesses angulaires de chacun des éléments.
Calculer les couples transmis par les trains épicycloïdaux
Le couple transmis est inversement proportionnel à la vitesse de rotation des deux éléments mobiles.
En entrant un couple d'entrée à l'élément menant, vous obtiendrez le couple de sortie reçu à l'élément mené.
Pour en savoir plus sur le couple et la puissance d'un mécanisme tournant et faire des calculs relatifs à ceux-ci, allez sur la page "Calcul de la Puissance et du couple".
Condition du nombre de dents
Il est nécessaire de respecter la condition du nombre de dents afin que le montage mécanique puisse se faire. Après avoir déduit le nombre de dents des pignons satellites, le moteur de calcul de cette page vérifie que cette condition soit respectée. Si vous obtenez un message "d'erreur" vous indiquant que cette condition n'est pas respectée, il suffit généralement d'augmenter ou de diminuer d'une dent l'un des deux planétaires. Faites plusieurs essais au besoin.
Autres conditions à respecter : La couronne doit posséder autant de dents que le nombre de dents du pignon central (dit "planétaire") additionné à ceux de deux pignons satellites.
De plus il sera nécessaire d'adapter le nombre de pignons satellites afin d'avoir un système équilibré, en respectant une autre condition : Le nombre de dents du pignon planétaire additionné au nombre de dents d'un pignon satellite, le tout divisé par le nombre de pignons satellites doit avoir pour résultat un nombre entier.
Cette dernière condition est elle aussi vérifiée dans le moteur de calcul, ce qui permet d'afficher le nombre optimal de pignons satellites dans les résultats.
Dans certains cas de figures, le résultat du nombre de dents des pignons satellites peut être très faible, voire trop faible. La limite minimale théorique est fixée à 3 dents par pignon. Pour être réaliste, il sera judicieux de réviser les données initiales afin que ce nombre de dents soit plus important, c'est-à-dire égal ou supérieur à 12.
Liste des pages de calculs
Argent
Automobile
Construction
Conversion
Divers
Electricité
Hydraulique
Informatique
Mathématiques
Arithmétique
Géométrie
Calculs des surfaces
Calculs des volumes et de leurs surfaces
Calculs des développantes
Trigonométrie
Mécanique
Santé
Sciences
Usinage