Calculer l'énergie et la vitesse maximale d'un volant d'inertie
Accumuler l'énergie cinétique
Les volants d'inertie sont des dispositifs mécaniques conçus pour stocker de l'énergie cinétique sous forme de rotation. Ils jouent un rôle clé dans de nombreuses applications, de la stabilisation des moteurs à la récupération d'énergie dans les systèmes mécaniques.
L'énergie stockée dépend de deux facteurs principaux :
- Moment d'inertie (I) : Dépend de la masse et de la répartition de celle-ci par rapport à l'axe de rotation.
- Vitesse angulaire (ω) : La vitesse de rotation, mesurée en radians par seconde.
Calculateur de Volant d'inertie
Ce calculateur vous permet d'évaluer leurs performances et leur sécurité.
Principe physique du volant d'inertie
Un volant d’inertie stocke l’énergie cinétique en mettant une masse en rotation autour d’un axe. L’énergie emmagasinée est donnée par la formule 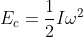 , où
, où 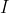 est le moment d’inertie (dépendant de la répartition de la masse par rapport à l’axe)
et
est le moment d’inertie (dépendant de la répartition de la masse par rapport à l’axe)
et 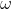 la vitesse angulaire (en radians par seconde). Le moment d’inertie dépend de la géométrie : pour un cylindre plein,
la vitesse angulaire (en radians par seconde). Le moment d’inertie dépend de la géométrie : pour un cylindre plein, 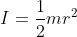 , et pour un cylindre creux,
, et pour un cylindre creux,
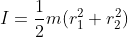 , où
, où 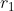 et
et 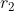 sont les rayons interne et externe. Comme
sont les rayons interne et externe. Comme 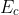 est proportionnelle à
est proportionnelle à
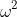 , doubler la vitesse quadruple l’énergie stockée, ce qui rend les hautes vitesses particulièrement intéressantes.
, doubler la vitesse quadruple l’énergie stockée, ce qui rend les hautes vitesses particulièrement intéressantes.
Pour restituer l’énergie, un moteur/générateur couplé au volant convertit l’énergie cinétique en électricité, ralentissant la rotation. En phase de stockage, le moteur accélère le volant ; en phase stationnaire, il compense les pertes par frottement pour maintenir la vitesse. Ce cycle charge/décharge est extrêmement rapide – de l’ordre de quelques millisecondes – et
offre un rendement élevé, souvent supérieur à 80 %.
Calculs Effectués
Moment d'inertie
Le moment d'inertie dépend de la géométrie du volant :
- Cylindre plein :
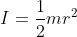 , où m est la masse et r le rayon.
, où m est la masse et r le rayon.
- Cylindre creux :
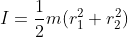 , où
, où 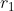 et
et 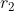 sont les rayons interne et externe.
sont les rayons interne et externe.
Calcul de l'énergie cinétique
- L'énergie cinétique est calculée par la formule :
 .
.
Les variables présentes dans les formules et leurs unités habituelles dans le système international (SI) :
Les unités utilisées dans les formules et leurs unités habituelles dans le système international sont issues du système international (SI)
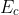 : énergie cinétique, mesurée en joules (J).
: énergie cinétique, mesurée en joules (J).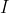 : moment d’inertie, mesuré en kilogrammes mètres carrés (kg·m²).
: moment d’inertie, mesuré en kilogrammes mètres carrés (kg·m²).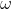 : vitesse angulaire, mesurée en radians par seconde (rad/s) (déjà mentionnée dans le texte).
: vitesse angulaire, mesurée en radians par seconde (rad/s) (déjà mentionnée dans le texte).- m : masse, mesurée en kilogrammes (kg).
- r,
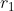 ,
, 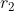 : rayons, mesurés en mètres (m).
: rayons, mesurés en mètres (m).
Les volants d'inertie, une technologie ancienne au service de l'avenir
Les volants d’inertie, ces dispositifs qui capturent l’énergie sous forme cinétique grâce à la rotation d’une masse, sont bien plus qu’une simple curiosité mécanique. Ils incarnent une solution élégante et robuste, née il y a des millénaires, qui trouve aujourd’hui sa place dans des applications modernes, de la gestion des réseaux électriques à la mobilité durable, en passant par des usages industriels et même domestiques. À l’image d’un croquis de Léonard de Vinci, où la simplicité apparente d’une roue massive cache une ingénierie complexe, les volants d’inertie méritent une exploration approfondie. Leur histoire, leurs applications, leurs avantages, leurs défis, et les technologies qui les entourent offrent un panorama fascinant pour quiconque s’intéresse à l’énergie, à la mécanique, ou à l’innovation durable.
Une histoire riche, des origines aux innovations modernes
Les volants d’inertie ne datent pas d’hier. Dès l’Antiquité, les potiers utilisaient des tours équipés de roues lourdes pour maintenir une rotation régulière, facilitant le façonnage de l’argile. Ce principe – une masse en rotation qui conserve son énergie – a traversé les siècles. À l’époque médiévale, les rouets à filer, utilisés pour produire du fil, intégraient des volants d’inertie pour lisser les mouvements irréguliers des artisans. Mais c’est avec la révolution industrielle, au XIXe siècle, que leur usage s’est véritablement démocratisé. Les machines à vapeur, comme celles des premières centrales électriques, étaient équipées de volants massifs pour compenser les à-coups des pistons et assurer une production d’électricité stable. On peut encore voir ces gigantesques volants dans certains musées industriels, témoins d’une époque où la mécanique régnait en maître.
Au XXe siècle, les volants d’inertie ont pris un tournant plus audacieux. Dans les années 1950, la société suisse Oerlikon a développé le Gyrobus, un autobus électrique fonctionnant grâce à un volant d’inertie de 1,5 tonne et 1,6 mètre de diamètre, tournant à 3000 tr/min. Ces véhicules, qui se rechargeaient en quelques minutes aux arrêts via une borne électrique, pouvaient parcourir 5 à 6 km par charge. Bien que techniquement impressionnants, les Gyrobus ont été abandonnés dans les années 1960 : leur poids, les risques liés à la rotation à grande vitesse, et la logistique des bornes de recharge ont eu raison de ce projet pionnier.
Plus près de nous, les volants d’inertie ont connu une renaissance avec des applications de pointe. En 2009, la Formule 1 a introduit les Systèmes de Récupération d’Énergie Cinétique (SREC), où des volants en fibre de carbone, tournant jusqu’à 64 000 tr/min, récupéraient l’énergie au freinage pour la restituer lors des accélérations. Des écuries comme Ferrari et McLaren ont ainsi gagné des secondes précieuses sur les circuits. Aujourd’hui, des entreprises comme Beacon Power aux États-Unis exploitent des centrales de 20 MW composées de 200 volants d’inertie pour stabiliser les réseaux électriques, tandis qu’en France, une société basée à Belfort fabrique des volants pour des applications industrielles et énergétiques. Par ailleurs, Energiestro, une start-up française, travaille sur des volants en béton pour démocratiser le stockage d’énergie solaire, prouvant que cette technologie ancienne a encore beaucoup à offrir.
Les technologies associées
Vide d’air et paliers magnétiques : Les frottements sont l’ennemi juré des volants d’inertie. Pour les minimiser, les systèmes modernes tournent dans une enceinte sous vide, parfois avec des paliers magnétiques qui éliminent tout contact physique. Energiestro, par exemple, vise des pertes de seulement 20 % sur 24 heures grâce à ces technologies. Cependant, maintenir un vide parfait demande des joints et des pompes à vide, ce qui augmente les coûts et nécessite un entretien régulier.
Contrôleurs de vitesse : À haute vitesse, un volant peut atteindre des contraintes mécaniques dangereuses. Des contrôleurs électroniques surveillent en temps réel la vitesse angulaire et ajustent le moteur/générateur pour rester dans une plage sûre. Ces systèmes sont essentiels pour éviter une rupture catastrophique, surtout avec des matériaux moins résistants comme le béton.
Transmission de l’énergie : L’énergie cinétique est transmise via un moteur/générateur couplé à l’axe. Dans les applications industrielles historiques, cette transmission était mécanique (via un embrayage), mais aujourd’hui, elle est électromécanique, convertissant l’énergie cinétique en électricité. La qualité de l’onduleur et du moteur est cruciale pour minimiser les pertes lors de la conversion.
Effet gyroscopique : Un volant en rotation génère un effet gyroscopique, qui peut être un défi dans des applications mobiles. Par exemple, dans un véhicule, un changement de direction peut induire des couples massifs sur les paliers, rendant la conduite instable. Des solutions comme les volants contra-rotatifs – utilisés dans les tramways Alstom Citadis – annulent cet effet. À l’inverse, cet effet est exploité dans des applications comme les actionneurs gyroscopiques de l’ISS, qui ajustent l’orientation de la station spatiale sans consommer de carburant.
Applications des volants d'inertie
Dans le domaine de l’énergie
Les volants d’inertie sont des alliés précieux pour la gestion des réseaux électriques, notamment avec l’essor des énergies renouvelables. Leur réactivité exceptionnelle (quelques millisecondes) en fait des outils idéaux pour la régulation de fréquence et la stabilisation des réseaux. Par exemple, la ville de New York utilise une centrale de 20 MW avec 200 volants d’inertie pour maintenir une alimentation stable en cas de chute de tension. Ils sont également utilisés pour lisser la production intermittente des éoliennes et des panneaux solaires. Cependant, leur coût de stockage (LCOS, Levelized Cost of Storage) est moins compétitif pour l’éolien que pour le solaire, selon André Gennesseaux d’Energiestro.
Energiestro développe des volants en béton (VOSS, Volant de Stockage Solaire) pour réduire les coûts. Le béton, bien que faible en traction, peut être comprimé pour supporter des vitesses élevées, divisant potentiellement par 10 le coût de stockage par rapport aux matériaux traditionnels. Ces volants visent une autonomie de 6 à 7 heures, parfaite pour l’autoconsommation solaire domestique. Imaginez un foyer équipé de panneaux solaires et d’un volant de 10 kWh : il pourrait stocker l’énergie produite le jour pour alimenter la maison la nuit, avec une puissance de 2 kW suffisante pour les besoins courants.
Dans l’industrie
Dans l’industrie, les volants d’inertie sont utilisés pour amortir les variations brutales de régime. Les concasseurs de gravier, par exemple, subissent des contraintes soudaines dues à la taille ou à la forme des roches. Un volant d’inertie stocke l’énergie cinétique nécessaire pour surmonter ces “points durs”, évitant au moteur de caler. De même, des machines comme les laminoirs ou les broyeurs intègrent des volants pour lisser les appels de puissance et se protéger des coupures électriques de courte durée. Dans les centrales hydroélectriques, les volants d’inertie historiques permettaient de maintenir une production stable face aux variations de débit d’eau.
Pour les particuliers
Pour un usage domestique, les volants d’inertie pourraient transformer l’autoconsommation. Un volant de 10 kWh, couplé à des panneaux solaires, pourrait fournir une autonomie quotidienne, avec une puissance de 2 kW suffisante pour une maison. Contrairement aux batteries, ils supportent des décharges profondes, voire totales, sans impact sur leur longévité, et leur durée de vie dépasse les 100 000 cycles (contre moins de 10 000 pour une batterie lithium-ion). Cependant, leur coût initial et leur encombrement restent des freins à une adoption massive. Energiestro travaille à résoudre ce problème avec ses volants en béton, mais le chemin est encore long avant une adoption généralisée.
Cependant, avec l’avènement des batteries LiFePO4, bien plus sûres que les batteries lithium-ion, même si leur espérance de vie reste inférieure à celle d’un volant d’inertie, ce dernier n’est plus vraiment compétitif. Mais il lui reste tout de même des avantages certains.
Avantages des volants d’inertie
Pourquoi les Adopter ?
Réactivité et efficacité : Les volants d’inertie peuvent charger et décharger en quelques secondes, avec un rendement de 80 % ou plus. Ils sont idéaux pour des applications nécessitant des pics de puissance, comme en Formule 1 ou pour stabiliser un réseau électrique.
Longévité exceptionnelle : Contrairement aux batteries, les volants ne se dégradent pas avec les cycles de charge/décharge. Leur durée de vie peut atteindre plusieurs décennies, limitée uniquement par l’usure mécanique des paliers. Avec des paliers magnétiques, cette usure est quasi inexistante.
Impact environnemental réduit : Les matériaux utilisés (acier, béton, composites) sont moins toxiques que ceux des batteries lithium-ion, et leur recyclage est plus simple. De plus, leur longévité réduit le besoin de remplacement fréquent.
Décharges profondes sans dommage : Un volant peut être totalement déchargé sans affecter sa performance, un avantage majeur par rapport aux batteries, qui perdent en capacité avec des décharges profondes.
Flexibilité d’application : Les volants d’inertie s’adaptent à une vaste gamme d’usages, du stockage d’énergie à grande échelle (centrales) à des applications locales (maisons, industries), en passant par des usages mobiles (véhicules, satellites).
Inconvénients et défis
Les limites à surmonter
Durée de stockage limitée : Les volants d’inertie sont conçus pour des stockages de courte durée (15 minutes à quelques heures). Les frottements, même réduits, entraînent des pertes d’énergie, rendant les stockages longue durée inefficaces. Ils sont donc complémentaires aux batteries, plutôt que concurrents directs.
Effet gyroscopique : À haute vitesse, un volant en rotation génère un effet gyroscopique qui peut compliquer son usage dans des systèmes mobiles. Par exemple, dans un véhicule, un changement de direction peut induire des couples massifs sur les paliers, rendant la conduite problématique. Des solutions comme les volants contra-rotatifs atténuent cet effet, mais augmentent la complexité et le coût.
Coût initial et encombrement : Bien que des matériaux comme le béton réduisent les coûts, les volants restent chers à produire et nécessitent des infrastructures robustes pour les hautes vitesses. Leur encombrement peut également poser problème, notamment pour un usage domestique.
Risques de rupture : À très haute vitesse, un volant mal équilibré ou fabriqué avec un matériau inadapté peut se briser, libérant une énergie colossale. Cela nécessite des enceintes de sécurité robustes, ce qui augmente encore les coûts.
Optimisation des volants d’inertie par le choix des matériaux
La performance d’un volant d’inertie dépend fondamentalement d’un compromis entre la densité du matériau et sa résistance mécanique. L’énergie stockée étant proportionnelle au carré de la vitesse de rotation, l’utilisation de matériaux légers mais résistants permet d’atteindre des capacités de stockage supérieures, malgré une masse réduite.
Principe clé
Un matériau deux fois moins dense nécessite un volume double pour une même masse. Cette augmentation de volume offre une section résistante plus grande, capable de supporter une vitesse de rotation accrue (multipliée par la racine de 2). L’énergie stockée, proportionnelle au carré de la vitesse, double alors.
Exemple concret
-
Un cylindre en fibre de carbone (densité : 1 500 kg/m³, résistance mécanique : 4 200 MPa) comparé à un cylindre en acier dits à ultra-haute résistance (UHSS tel que l'acier martensitique Docol® - densité : 7 800 kg/m³, résistance mécanique environ 1 000 MPa).
-
La fibre, cinq fois moins dense mais quatre fois plus résistante, permet une vitesse périphérique maximale de 2 366 m/s contre 506 m/s pour l’acier.
-
Résultat : une densité énergétique 22 fois supérieure (638 Wh/kg contre 29 Wh/kg).
Avantages des matériaux légers
-
Compensation masse/vitesse : La réduction de masse est compensée par une vitesse accrue, sans augmentation des contraintes mécaniques (la force centrifuge dépend de la densité et du carré de la vitesse de rotation, équilibrée par la section résistante).
-
Efficacité énergétique : Un volant en composite stocke jusqu’à 26,7 kWh contre 6,3 kWh pour l’acier à volume égal.
-
Durabilité : Les composites résistent mieux à la fatigue cyclique, avec une durée de vie dépassant 20 ans.
Défis pratiques
-
Coûts : Les composites (fibre de carbone) et les systèmes de lévitation magnétique augmentent l’investissement initial.
-
Technologie : Les vitesses élevées (plus de 50 000 tr/min) exigent un vide poussé et un équilibrage dynamique parfait.
Conclusion
Le choix optimal dépend du contexte d’utilisation :
-
Applications stationnaires (réseaux électriques) : privilégient les matériaux légers à haute résistance pour maximiser l’énergie stockée.
-
Mobilité (véhicules) : favorise les compromis coût/poids, comme l’aluminium.
Cette approche explique pourquoi les volants haute vitesse en composites dominent désormais le stockage inertiel, malgré leur complexité.
Cependant...
L’acier, un intéressant rapport coût/performance
L’acier est un matériau traditionnel pour les volants d’inertie, utilisé depuis des siècles dans les machines industrielles. Bien qu’il ait une résistance spécifique plus faible que la fibre de carbone (environ 45 kJ/kg contre 1250 kJ/kg), il offre un rapport coût/performance imbattable. À environ 1 à 2 €/kg, contre 50 à 100 €/kg pour la fibre de carbone, l’acier permet de stocker plus d’énergie par euro investi. Dans les applications stationnaires, comme le stockage d’énergie domestique ou industriel, le poids n’est pas une contrainte, et la densité élevée de l’acier réduit l’encombrement volumique : pour une masse donnée, un volant en acier sera plus compact qu’un volant en fibre de carbone. Enfin, la mise en forme de l’acier (usinage, forgeage) est bien maîtrisée et économique, ce qui en fait un choix privilégié pour des applications à grande échelle.
Malheureusement pour lui, sa densité est plus un inconvénient qu'un avantage. Car, comme nous l'avons vu précédemment, plus un matériau est léger plus il nécessite de volume à masse égale, ce qui lui procure d'autant plus de capacité de résistance.
La fibre de carbone : pour les applications de pointe
Les matériaux composites, comme la fibre de carbone, dominent les applications nécessitant un faible poids, notamment dans les systèmes mobiles. Avec une résistance spécifique bien supérieure, ils permettent de tourner à des vitesses extrêmes (jusqu’à 100 000 tr/min dans certains cas) sans risque de rupture, stockant plus d’énergie par kilogramme. En Formule 1, par exemple, les volants en fibre de carbone du SREC tournaient à 64 000 tr/min, stockant une énergie colossale dans un volume réduit. Cependant, leur coût élevé et la complexité de leur fabrication (tissage, stratification, polymérisation) limitent leur usage aux applications où le gain en performance – et surtout la réduction de poids – justifie l’investissement, comme dans les véhicules ou les satellites.
Le béton : une innovation prometteuse
Energiestro, une start-up française, explore une voie originale avec des volants en béton. Bien que le béton ait une faible résistance en traction, il peut être comprimé pour supporter des vitesses élevées. Cette approche divise par 10 le coût de stockage par rapport aux matériaux traditionnels, rendant les volants d’inertie accessibles pour des applications domestiques, comme le stockage d’énergie solaire. Cependant, le béton a une résistance spécifique très faible, ce qui impose des vitesses plus modestes et donc une énergie stockée moindre par kilogramme, même si son faible coût compense cet inconvénient dans des applications stationnaires.
Autres matériaux : titane, aramide, et au-delà
Des matériaux comme le titane ou les fibres d’aramide (Kevlar) offrent un excellent rapport résistance/poids, mais leur coût prohibitif les réserve à des applications de niche, comme les satellites ou les systèmes militaires. Dans les années 1970, des recherches ont exploré des volants en alliages exotiques, mais les coûts et les difficultés d’équilibrage ont freiné leur adoption. Aujourd’hui, la recherche se concentre sur des matériaux hybrides, combinant par exemple des fibres de carbone et des résines innovantes, pour améliorer la résistance tout en réduisant les coûts.
Équilibrage et maintenance : les clés d’une longévité infinie
L’importance de l’équilibrage
À haute vitesse, un volant d’inertie doit être parfaitement équilibré pour éviter les vibrations, qui peuvent endommager les paliers ou provoquer une rupture. Un déséquilibre, même minime, génère des forces oscillantes proportionnelles au carré de la vitesse angulaire, ce qui peut être catastrophique à 50 000 tr/min. L’équilibrage nécessite des machines de précision pour ajuster la répartition des masses, un processus coûteux mais essentiel. Par exemple, les volants en fibre de carbone de Formule 1 étaient équilibrés au milligramme près pour garantir leur stabilité à des vitesses extrêmes.
Une maintenance réduite mais nécessaire
Un volant bien conçu demande peu de maintenance. Les paliers magnétiques éliminent l’usure par contact, et l’absence de réactions chimiques (comme dans les batteries) garantit une longévité exceptionnelle – souvent plusieurs décennies. Cependant, certains éléments nécessitent une attention périodique : les joints du vide, qui peuvent s’user et compromettre l’étanchéité, et les contrôleurs électroniques, qui doivent être calibrés pour éviter les dérives. Avec un entretien minimal, un volant d’inertie peut fonctionner indéfiniment, ce qui en fait une solution durable par excellence.
Volants d’inertie vs batteries, une comparaison éclairante
Les volants d’inertie offrent des avantages uniques par rapport aux batteries électrochimiques. Ils supportent des décharges profondes, voire totales, sans aucun impact sur leur longévité, alors qu’une batterie lithium-ion perd en capacité si elle est déchargée à 0 %. Leur durée de vie dépasse les 100 000 cycles, contre moins de 10 000 pour une batterie. De plus, leur impact environnemental est moindre : les matériaux (acier, béton, composites) sont moins toxiques et plus faciles à recycler que le lithium ou le cobalt. Cependant, leur incapacité à stocker l’énergie sur de longues périodes les rend complémentaires aux batteries, plutôt que concurrents directs. Par exemple, un volant peut gérer les pics de puissance sur un réseau, tandis qu’une batterie assure un stockage longue durée.
Perspectives et innovations
Dans l’énergie renouvelable
Avec l’essor des énergies renouvelables, les volants d’inertie ont un rôle clé à jouer. Leur réactivité et leur capacité à gérer des pics de puissance en font des outils idéaux pour stabiliser les réseaux alimentés par des sources intermittentes comme le solaire ou l’éolien. Des projets comme ceux de Beacon Power ou d’Energiestro montrent que les volants peuvent être intégrés à grande échelle, mais aussi à l’échelle domestique, pour l’autoconsommation.
Dans la mobilité
Dans les transports, les volants d’inertie reviennent sur le devant de la scène. Les tramways Alstom Citadis utilisent des volants pour réduire leur dépendance aux caténaires, tandis que des concepts comme le Gyrobus pourraient être revisités avec des matériaux modernes. Cependant, l’effet gyroscopique reste un défi majeur pour les véhicules mobiles, nécessitant des innovations comme les volants contra-rotatifs ou des systèmes de suspension avancés.
Dans l’espace
Dans l’espace, les volants d’inertie sont déjà utilisés pour des applications uniques. Les actionneurs gyroscopiques de l’ISS, par exemple, exploitent l’effet gyroscopique pour ajuster l’orientation de la station sans consommer de carburant. À l’avenir, des volants pourraient stocker l’énergie solaire dans l’espace, alimentant des satellites ou des bases lunaires avec une fiabilité inégalée.
Conclusion - Une technologie intemporelle
Les volants d’inertie, nés il y a des millénaires, continuent de fasciner par leur simplicité et leur potentiel. Comme un croquis de Léonard de Vinci, ils incarnent l’élégance de la mécanique pure, tout en s’adaptant aux défis du XXIe siècle. Leur capacité à stocker et restituer l’énergie rapidement, leur longévité exceptionnelle, et leur impact environnemental réduit en font une solution d’avenir pour la gestion de l’énergie, l’industrie, et même les particuliers. Cependant, des défis comme l’effet gyroscopique, le coût initial, et la durée de stockage limitée nécessitent encore des avancées technologiques. En attendant, ce calculateur vous permet d’explorer leurs performances et de vérifier leur sécurité, que vous soyez un ingénieur, un bricoleur, ou un curieux de la mécanique. Pour des applications critiques, n’hésitez pas à consulter un spécialiste en résistance des matériaux – car derrière la simplicité d’un volant se cache une science complexe, prête à tourner pour les générations futures.
Liste des pages de calculs
Argent
Automobile
Construction
Conversion
Divers
Electricité
Hydraulique
Informatique
Mathématiques
Arithmétique
Géométrie
Calculs des surfaces
Calculs des volumes et de leurs surfaces
Calculs des développantes
Trigonométrie
Mécanique
Santé
Sciences
Usinage